EN ESTA PARTE ENCONTRARAS INFORMACIÓN ACERCA DE LOS NÚMEROS FRACCIONARIOS: SUMA, RESTA, MULTIPLICACIÓN Y DIVISIÓN.
Los Números fraccionarios. Se encuentran dentro del conjunto de los números racionales (Q) y se expresan de las forma a/b o como una expresión decimal periódica.
Surgen por la necesidad de dar solución a la división en el conjunto de los números naturales.
Los números están en cada una de las acciones de la vida cotidiana y con ellos podemos contar, ordenar, medir y comparar dos o varias cantidades.
Para cada acción siempre se utilizan diferentes tipos de números.
Un mismo número puede representar cantidades diferentes de acuerdo con su significado, y en otras ocasiones, números expresados de formas diferentes pueden tener el mismo significado.
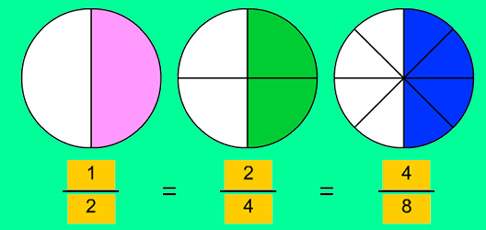
Diferentes números expresando la misma cantidad.
A partir de las diferentes operaciones de cálculo que podemos realizar con los números, han ido surgiendo los conjuntos numéricos y dentro de ellos los el de los números fraccionarios.
Definición
Los números fraccionarios o fracciones comunes se forman al plantear una división entre dos números naturales, teniendo en cuenta que siempre el divisor debe ser diferente de cero.
En un número fraccionario o fracción, el denominador indica las partes en que se divide la unidad y el numerador indica las partes que se toman.
Formas de expresión
Una fracción puede considerarse como el cociente exacto de dividir el numerador entre el denominador, de ahí que se pueda escribir también como el cociente a : b.
Una fracción representa un número natural cuando al dividir el numerador por el denominador el resto de la división es cero.
Las fracciones comunes se pueden expresar en notación decimal. El número que se encuentra a la izquierda de la coma es la parte entera y las cifras que quedan situadas a la derecha de la coma son la parte decimal. La primera cifra después de la coma representa las décimas, la segunda las centésimas, la tercera las milésimas y así sucesivamente.
10 décimas forman una unidad, 10 centésimas forman una décima y 10 milésimas forman una centésima. Luego una unidad tiene 10 centésimas, 100 centésimas y 1000 milésimas.
También existen las fracciones propias y las impropias:
Una fracción se llama propia si su numerador es menor que su denominador.
Una fracción se llama impropia si su numerador es mayor que su denominador. Se puede expresar como un número mixto formado por un número natural más una fracción propia.
Si el numerador de una fracción es múltiplo del denominador, la fracción representa un número natural.
Representación de los números fraccionarios sobre una recta numérica
Las fracciones propias o expresiones decimales cuya parte entera es cero, siempre estarán situadas entre 0 y 1. Para representarlas se divide la unidad en tantas partes iguales como indique el denominador y posteriormente se determina el punto que representa las partes que indica el numerador. Si la fracción es un medio, la unidad se divide en dos partes iguales y el punto que corresponde a esa fracción es el que indica la mitad de la unidad. Para representar en la recta numérica una expresión decimal se puede expresar como fracción común (aunque no es necesario).
En muchas ocasiones se ubica por su significado. Las fracciones impropias, que pueden aparecer representadas como números mixtos o expresiones decimales donde la parte entera es diferente de cero, siempre se ubican en la recta numérica a la derecha de 1. Para ello se ubica primero el punto correspondiente a la parte entera y a partir de él, se determina en qué punto de la próxima unidad está ubicada la fracción o parte decimal del número, siendo este último, el lugar de la recta numérica donde queda situado este número fraccionario o fracción.
El menor número fraccionario es cero pero entre un número fraccionario y otro existen infinitos números más, luego no tienen antecesor ni sucesor. Se dice que este dominio numérico es un dominio denso.
Ordenar y comparar números fraccionarios expresados en diferentes formas
Al igual que en los números naturales, de dos fracciones es menor la que se encuentre situada más a la izquierda en la recta numérica.
Existen varias maneras de comparar números fraccionarios (o fracciones comunes).
De dos fracciones que tienen igual numerador es menor la que tenga mayor denominador.
Las fracciones de igual denominador mantienen la misma relación de orden que sus numeradores.
Cuando dos fracciones tienen diferentes numeradores y denominadores para su comparación se debe conocer que:
Toda fracción propia es menor que 1 y que cualquier fracción impropia.
Si las dos son propias o las dos son impropias se aplica el procedimiento del producto cruzado.
Adición y sustracción de números fraccionarios
En caso de las expresiones decimales la adición y la sustracción se calculan como si fueran números naturales, escribiendo la coma debajo de la coma de modo que las unidades del mismo orden queden una debajo de la otra.
Para facilitar el cálculo en una sustracción donde el minuendo tenga menos cifras decimales que el sustraendo, se añaden al primero tantos ceros hasta igualar la cantidad de cifras decimales de ambos elementos y en el resultado se escribe la coma en el mismo lugar que ocupa en los elementos de la adición o sustracción.
Para adicionar fracciones de igual denominador, se adicionan los numeradores y se mantiene el mismo denominador.
Para sustraer fracciones de igual denominador, al numerador del minuendo se le sustrae el numerador del sustraendo y se mantiene el mismo denominador.
En ambas operaciones el resultado se simplifica si es posible.
Para adicionar o sustraer fracciones de diferente denominador se calcula el mínimo común múltiplo (m.c.m) de los denominadores, se amplían los numeradores y luego se adicionan o se sustraen, manteniendo en el resultado el denominador. El resultado se simplifica si es posible.
La adición de números naturales y fraccionarios es conmutativa y asociativa.
El conocimiento de estas propiedades nos permite aplicarlas para realizar cálculos de una forma más ventajosa.
La sustracción de números naturales y fraccionarios por su parte, no es conmutativa ni asociativa.
Multiplicación y división de números fraccionarios
Multiplicación.
Los Números fraccionarios. Se encuentran dentro del conjunto de los números racionales (Q) y se expresan de las forma a/b o como una expresión decimal periódica.
Surgen por la necesidad de dar solución a la división en el conjunto de los números naturales.
Los números están en cada una de las acciones de la vida cotidiana y con ellos podemos contar, ordenar, medir y comparar dos o varias cantidades.
Para cada acción siempre se utilizan diferentes tipos de números.
Un mismo número puede representar cantidades diferentes de acuerdo con su significado, y en otras ocasiones, números expresados de formas diferentes pueden tener el mismo significado.

Diferentes números expresando la misma cantidad.
A partir de las diferentes operaciones de cálculo que podemos realizar con los números, han ido surgiendo los conjuntos numéricos y dentro de ellos los el de los números fraccionarios.
Definición
Los números fraccionarios o fracciones comunes se forman al plantear una división entre dos números naturales, teniendo en cuenta que siempre el divisor debe ser diferente de cero.
En un número fraccionario o fracción, el denominador indica las partes en que se divide la unidad y el numerador indica las partes que se toman.
Formas de expresión
Una fracción puede considerarse como el cociente exacto de dividir el numerador entre el denominador, de ahí que se pueda escribir también como el cociente a : b.
Una fracción representa un número natural cuando al dividir el numerador por el denominador el resto de la división es cero.
Las fracciones comunes se pueden expresar en notación decimal. El número que se encuentra a la izquierda de la coma es la parte entera y las cifras que quedan situadas a la derecha de la coma son la parte decimal. La primera cifra después de la coma representa las décimas, la segunda las centésimas, la tercera las milésimas y así sucesivamente.
10 décimas forman una unidad, 10 centésimas forman una décima y 10 milésimas forman una centésima. Luego una unidad tiene 10 centésimas, 100 centésimas y 1000 milésimas.
También existen las fracciones propias y las impropias:
Una fracción se llama propia si su numerador es menor que su denominador.
Una fracción se llama impropia si su numerador es mayor que su denominador. Se puede expresar como un número mixto formado por un número natural más una fracción propia.
Si el numerador de una fracción es múltiplo del denominador, la fracción representa un número natural.
Representación de los números fraccionarios sobre una recta numérica
Las fracciones propias o expresiones decimales cuya parte entera es cero, siempre estarán situadas entre 0 y 1. Para representarlas se divide la unidad en tantas partes iguales como indique el denominador y posteriormente se determina el punto que representa las partes que indica el numerador. Si la fracción es un medio, la unidad se divide en dos partes iguales y el punto que corresponde a esa fracción es el que indica la mitad de la unidad. Para representar en la recta numérica una expresión decimal se puede expresar como fracción común (aunque no es necesario).
En muchas ocasiones se ubica por su significado. Las fracciones impropias, que pueden aparecer representadas como números mixtos o expresiones decimales donde la parte entera es diferente de cero, siempre se ubican en la recta numérica a la derecha de 1. Para ello se ubica primero el punto correspondiente a la parte entera y a partir de él, se determina en qué punto de la próxima unidad está ubicada la fracción o parte decimal del número, siendo este último, el lugar de la recta numérica donde queda situado este número fraccionario o fracción.
El menor número fraccionario es cero pero entre un número fraccionario y otro existen infinitos números más, luego no tienen antecesor ni sucesor. Se dice que este dominio numérico es un dominio denso.
Ordenar y comparar números fraccionarios expresados en diferentes formas
Al igual que en los números naturales, de dos fracciones es menor la que se encuentre situada más a la izquierda en la recta numérica.
Existen varias maneras de comparar números fraccionarios (o fracciones comunes).
De dos fracciones que tienen igual numerador es menor la que tenga mayor denominador.
Las fracciones de igual denominador mantienen la misma relación de orden que sus numeradores.
Cuando dos fracciones tienen diferentes numeradores y denominadores para su comparación se debe conocer que:
Toda fracción propia es menor que 1 y que cualquier fracción impropia.
Si las dos son propias o las dos son impropias se aplica el procedimiento del producto cruzado.
Adición y sustracción de números fraccionarios
En caso de las expresiones decimales la adición y la sustracción se calculan como si fueran números naturales, escribiendo la coma debajo de la coma de modo que las unidades del mismo orden queden una debajo de la otra.
Para facilitar el cálculo en una sustracción donde el minuendo tenga menos cifras decimales que el sustraendo, se añaden al primero tantos ceros hasta igualar la cantidad de cifras decimales de ambos elementos y en el resultado se escribe la coma en el mismo lugar que ocupa en los elementos de la adición o sustracción.
Para adicionar fracciones de igual denominador, se adicionan los numeradores y se mantiene el mismo denominador.
Para sustraer fracciones de igual denominador, al numerador del minuendo se le sustrae el numerador del sustraendo y se mantiene el mismo denominador.
En ambas operaciones el resultado se simplifica si es posible.
Para adicionar o sustraer fracciones de diferente denominador se calcula el mínimo común múltiplo (m.c.m) de los denominadores, se amplían los numeradores y luego se adicionan o se sustraen, manteniendo en el resultado el denominador. El resultado se simplifica si es posible.
La adición de números naturales y fraccionarios es conmutativa y asociativa.
El conocimiento de estas propiedades nos permite aplicarlas para realizar cálculos de una forma más ventajosa.
La sustracción de números naturales y fraccionarios por su parte, no es conmutativa ni asociativa.
Multiplicación y división de números fraccionarios
Multiplicación.
Para multiplicar expresiones decimales donde se calcula el producto como si los factores fueran números naturales y en el resultado se ubica la coma decimal contando a partir de la derecha tantos lugares decimales como haya en los dos factores juntos.
En el caso de que los factores sean fracciones, se simplifica si es posible y luego se multiplica numerador con numerador y denominador con denominador. También puede multiplicarse primero y después simplificar el resultado.
La multiplicación de números naturales y fraccionarios es conmutativa y asociativa, y al igual que en la adición, la aplicación de estas propiedades puede resultar ventajosa para el cálculo.
Para dividir un número natural entre una expresión decimal (123 : 0,6) o una expresión decimal entre otra (1,02 : 0,5) se procede a transformar la división para eliminar la coma del divisor. Para lograrlo se multiplica el dividendo y el divisor por 10, 100, 1000,… según la cantidad de lugares decimales que tenga divisor y se procede a hacer la división.
Otra forma sería multiplicar dividendo y divisor por 10, 100, 1000,… atendiendo a la cantidad de lugares decimales del que mayor cantidad de estas cifras tenga. Luego se dividen los números naturales que se obtienen.
Al terminar de dividir todos los dígitos que tiene el dividendo, si la división no resulta exacta, se coloca la coma decimal en el cociente para poder continuar la división.
División
En el caso de la división de fracciones se procede de la siguiente forma:
La división se expresa como la multiplicación del dividendo por el recíproco del divisor.
Se resuelve la multiplicación indicada.
En el caso de que alguna de las fracciones originales tenga simplificación podemos realizarla antes de realizar el primer paso.
La multiplicación de números naturales y fraccionarios es conmutativa y asociativa, y al igual que en la adición, la aplicación de estas propiedades puede resultar ventajosa para el cálculo.
Para dividir un número natural entre una expresión decimal (123 : 0,6) o una expresión decimal entre otra (1,02 : 0,5) se procede a transformar la división para eliminar la coma del divisor. Para lograrlo se multiplica el dividendo y el divisor por 10, 100, 1000,… según la cantidad de lugares decimales que tenga divisor y se procede a hacer la división.
Otra forma sería multiplicar dividendo y divisor por 10, 100, 1000,… atendiendo a la cantidad de lugares decimales del que mayor cantidad de estas cifras tenga. Luego se dividen los números naturales que se obtienen.
Al terminar de dividir todos los dígitos que tiene el dividendo, si la división no resulta exacta, se coloca la coma decimal en el cociente para poder continuar la división.
División
En el caso de la división de fracciones se procede de la siguiente forma:
La división se expresa como la multiplicación del dividendo por el recíproco del divisor.
Se resuelve la multiplicación indicada.
En el caso de que alguna de las fracciones originales tenga simplificación podemos realizarla antes de realizar el primer paso.
Suma de fracciones con igual denominador
Cuando tenemos dos o más fracciones con el mismo denominador, se suman los numeradores y se mantiene el mismo denominador.
Ejemplo:
Ejemplo:
|
Para saber qué cantidad vendió en total, María hace la suma de fracciones de la siguiente manera:
Observa las siguientes figuras.
Ejemplo 2: Si queremos sumar las fracciones:
|









No hay comentarios.:
Publicar un comentario